日本天文考古学会 学会誌 創刊号『J-AASJ』vol.1 2019年12月1日発行
東亜天文学会誌『天界』2019年10,12月号 2020年4,6,7,9,11月号 2021年3,10月号連載
前漢の二十八宿天体暦 汝陰侯墓出土円儀の天文学的考察
<西汉二十八宿天体历书 天文学的考察在汝阴侯墓出土圆仪>
The ephemerides of the twenty-eight lunar mansions in the Former Han
Astronomical study on the round instruments from the tomb of the Marquis of Ruyin
日本天文考古学会・東亜天文学会 江頭 務 Tsutomu Egashira
Up to now, the three round instruments < Rikujin form disk(六壬式盤),
Taiitsu nine palaces disk(太乙九宮占盤), the twenty-eight lunar mansions disk(二十八宿円盤)>
from the tomb of the Marquis of Ruyin have been studied individually
on the history of Chinese astronomy.
This paper simulated the twenty-eight lunar mansions using astronomy software
under an assumption that the three round instruments discovered
from the same tomb have close astronomical relations.
As a result, the calendar of Rikujin form disk followed the equal dividing method
on the twenty four seasonal datum points indicated by Taiitsu nine palaces disk.
Rikujin form disk displayed the twenty-eight lunar mansions
at the midnight (0:00am) which is the first time on a day in ancient China.
And the twenty-eight lunar mansions disk made it clear to possess
the function of the present star chart disk which makes the South Pole in heaven the revolving center.
1.はじめに
<要旨>
中国天文学史に必ず登場するといっても過言ではない
前漢時代の汝陰侯墓より出土した三つの円儀(六壬式盤・太乙九宮占盤・二十八宿円盤)は、これまで個別に検討されてきた。
本論文は同じ墓から出土した三つの円儀は天文学的に密接な関係を有しているとの想定のもとに、
天文ソフトを使い二十八宿のシミュレーションを行ったものである。
その結果、六壬式盤の天盤の暦は太乙九宮占盤の冬至起算の平気法による節切りを踏襲したものであり、
古代中国における一日の始まりである夜半(午前0時)に展開している二十八宿を表示しているとの結論を得た。
また、二十八宿円盤は天の南極を回転の中心とする現在の星座早見盤の機能を有していることを明らかにした。
1 はじめに
天体暦とは、日本天文学会の『天文学辞典』(HP1)によれば、
「月、太陽、惑星、小惑星、恒星などの天体の位置を天体力学の理論に基づいて計算し、時刻の関数として表したもの」とある。
これを古代に適用するならば、天体と時刻の関係を示した遺物も広義の歴史的解釈として天体暦に含めてもよいであろう。
ここでは中国天文学史にしばしば登場する汝陰侯墓(じょいんこうぼ)から出土した下記の遺物を取り上げる。
三円儀(さんえんぎ)
・六壬式盤(りくじんしょくばん)(略称:式盤)(注)
・太乙九宮占盤(たいいつきゅうきゅうせんばん)(略称:九宮盤)
・二十八宿円盤(略称:宿盤)
(注)式盤の読みは、「ちょくばん」「しきばん」が多数派であるが、
本稿は精緻な研究を行っている山田慶兒の「しょくばん」(文献1①)を採用した。
1977年7月、中国安徽(あんき)省阜陽(ふよう)県にある前漢初期の汝陰侯墓から、
二十八宿の名が記載された最古の六壬式盤(図1)が発見された。
また同時に、冬至の年と八節間の日数が記載された太乙九宮占盤(図2)と
二十八宿の度数が記載された二十八宿円盤(図3)が出土した。(文献2)
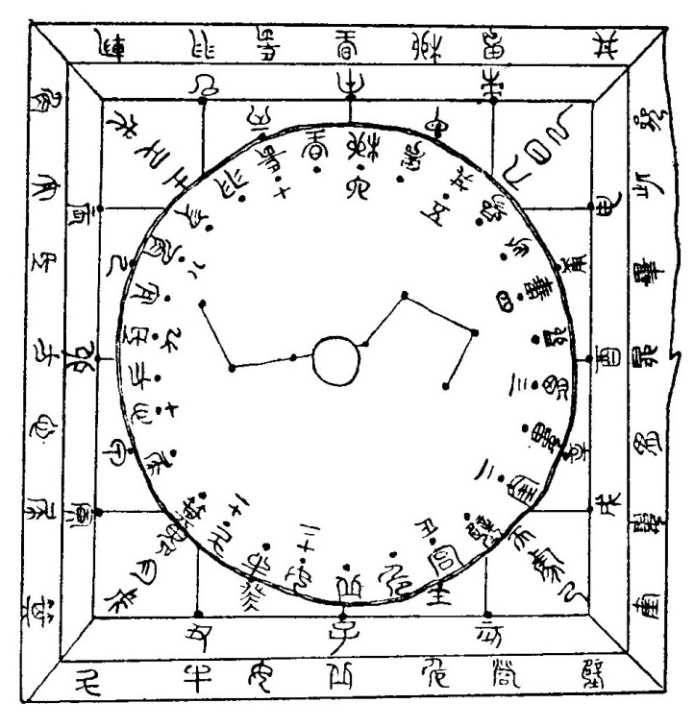
図1 前漢汝陰侯墓出土の六壬式盤(略称:式盤)(文献3)
天盤(円形) 直径9.3㎝ 厚さ0.6cm 地盤 (正方形) 一辺13.5cm 厚さ1.2cm
 |
|
| 表面 | 裏面 |
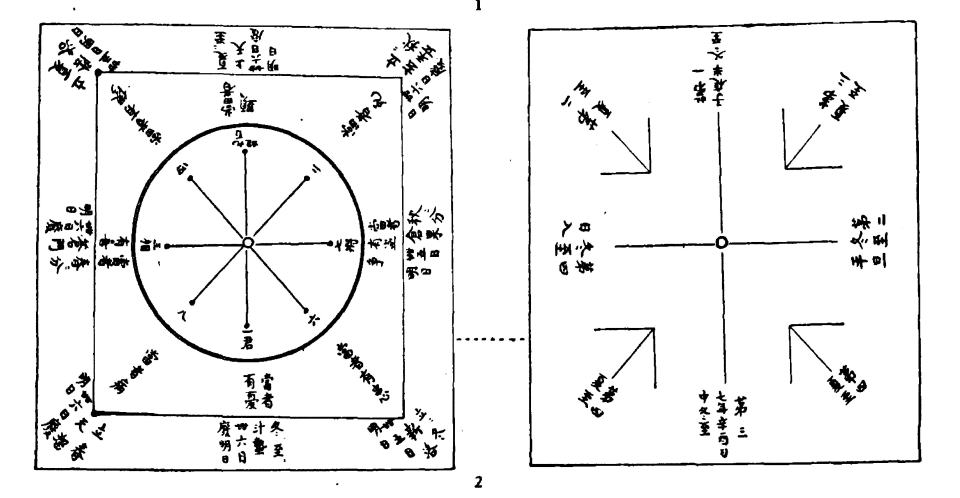
図2 前漢汝陰侯墓出土の太乙九宮占盤(略称:九宮盤) 解説図(文献3)
表面 上盤(円形) 直径8cm 厚さ0. 2cm 下盤(正方形) 一辺14.5 cm 厚さ1.7cm
下盤外周に八節の名と八節間の日数が記載されている。
裏面 中央下部には文帝七年(BC173年)とされる「七年辛酉(しんゆう)日中冬至」の文字が見える。
 |
|
| 摹本(もほん) | 翻刻 |
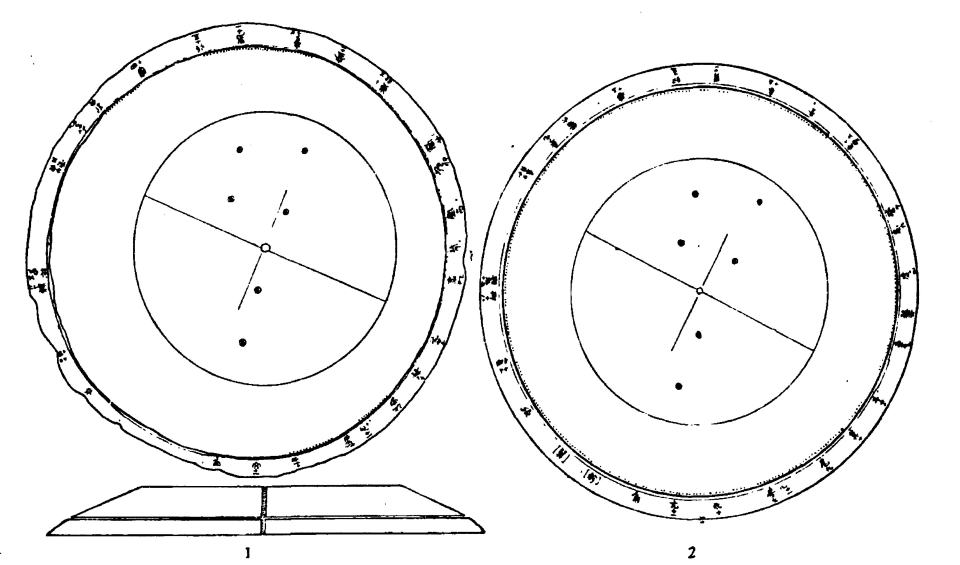
図3 前漢汝陰侯墓出土の二十八宿円盤(略称:宿盤)(文献3)
上盤(円形) 外径23.0cm 厚さ1.7cm 下盤(円形) 外径25.6cm 厚さ0. 8cm
発掘の報告書としては「阜陽双古堆西漢汝陰侯墓発掘簡報」(文献2)1978があるが、
考古学的な遺物としての簡単な紹介である。
最初にこれらの三つの円儀を天文儀器として検討したのは殷涤非(いんじょうひ)であった。
殷涤非の論文「西漢汝陰侯墓出土的占盤和天文円儀」(文献3)1978において、
九宮盤の八節間の日数、宿盤の二十八宿の度数が報告された。
さらに、宿盤の二十八宿の度数について再吟味し、洪範伝古度との類似性を指摘したのは
潘鼐(はんだい)「我國早期的二十八宿觀測及其時代考」(文献4)1979である。
我が国においては、橋本敬造が「先秦時代の星座と天文觀測」(HP2)1981の中で潘鼐の論文を引用している。
最新の研究としては、山田慶兒の『制作する行為としての技術』(文献1)1991が
三つの円儀を主として占術の視点から総合的にまとめている。
しかしながらこれまでの天文学的視点からの研究は、八節間の日数、宿盤の二十八宿の度数についての
論議があるのみで、式盤と宿盤の具体的な操作における天文学上の結果については述べられていないのが実情である。
本稿は、これらの三つの円儀が天文学的に密接な関係を有しており、六壬式盤が暦については太乙九宮占盤、
二十八宿の運行については二十八宿円盤をデータベースとして成立していることを明らかにしたものである。
<検討の前提条件>
1 暦はグレゴリオ暦を基準とするが、1582年10月4日以前の暦はユリウス暦を使用する。
2 時刻系は、ユリウス暦の場合は太陽の南中を12時とする視太陽時を使用する。
また均時差曲線の日々の変化量として表れる太陽の南中から次の日の南中までに要する時間差は、
BC173年において最大でも冬至の頃に平均太陽時の24時間に対し+31秒なので、
ここでは太陽南中時の12時間前をその日の午前0時とする。
3 星空の観測地は、汝陰侯墓のある中国阜陽(ふよう)市 北緯32.9°東経115.8°とする。
4 二十八宿は距星で代表させる。
5 二十八宿のシミュレーションは天文ソフト:ステラナビゲータ10(アストロアーツ)、計算とグラフはエクセルを使用する。
尚、上記天文ソフトにおいてはデータ取得のタイミング等により2s 程度の変動が認められる。
6 検討対象となる星空は、汝陰侯墓から出土した太乙九宮占盤の銘の推定年である
文帝七年冬至を起算日とした紀元前173年から171年とする。
7 古代中国の星の観測に用いられる度数は「度」、現在の天文学に用いられる角度の単位は「°」で表記する。
2 六壬式盤について
六壬式は平安時代から鎌倉時代にかけて陰陽道の必須の占術であり、
陰陽師として名高い安倍晴明は子孫のために『占事略决』(文献5、6)を残している。
六壬式盤は、天盤と呼ばれる円形の盤と地盤と呼ばれる正方形の盤を組み合わせたもので、
円形の天盤が回転する構造となっている。
天盤や地盤の形状は、古代中国の宇宙観である天円地方説に基づいている。
図4は前漢末期の武威磨咀子(ぶいまそし)三座漢墓より出土した六壬式盤の解説図である。
天盤の中央には裏向けの北斗七星、その外側には月将と呼ばれる正月から十二月に対応する神名が記載されている。
さらに、その外側には二十八宿が均等に配置されている。
地盤には、方位と時刻を同時に表す十二支、その間に十干がある。
尚、戊と己は記載されていないが四維(しい)に2回ずつ配当される。(天盤の月将功曹と大吉の間に戊の文字が見える)
そして外周には二十八宿が東西南北に七宿ずつにわけて配置されている。
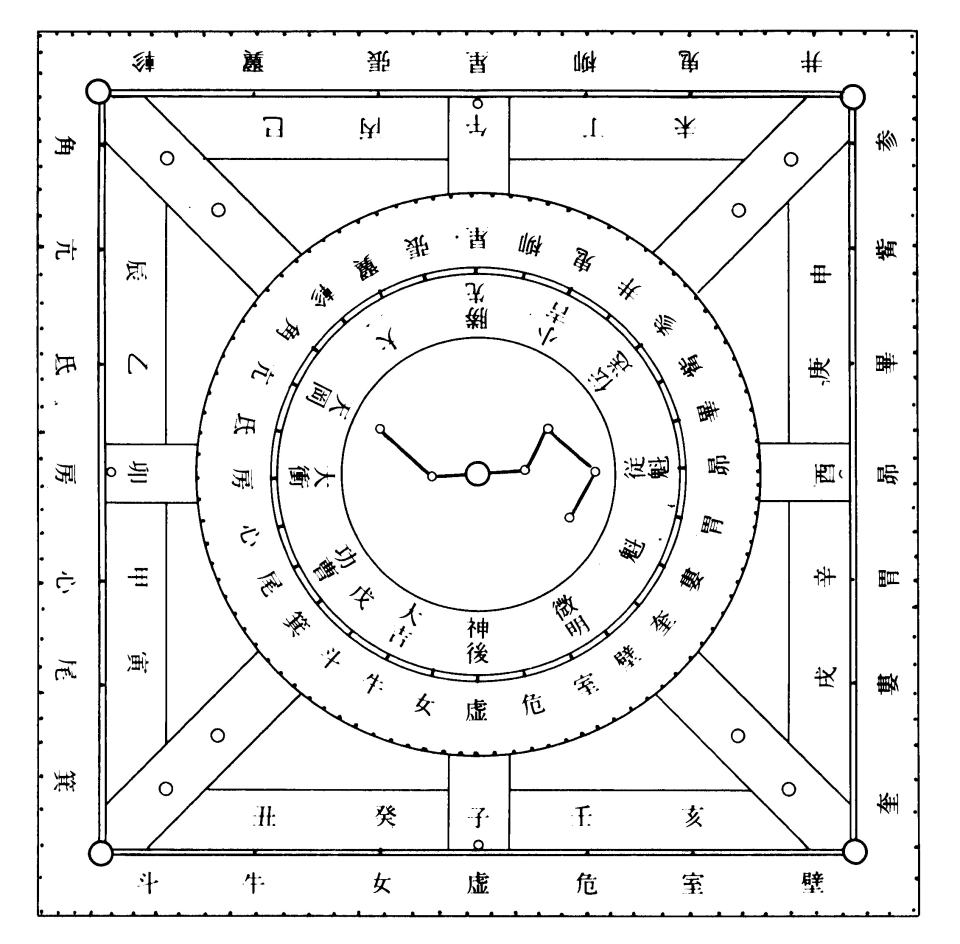
図4 武威磨咀子(ぶいまそし)三座漢墓出土六壬式盤の解説図(文献1②)(注)
出土品の寸法(文献7) 天盤(円形) 直径6㎝ 地盤(正方形) 一辺9cm 全高1㎝
(注)ほとんどの書は、式盤の子(北)を上方に記載しているが、午(南)を上にするのが正統である。
『神定経』巻二・釈用式に引く『金匱経(きんききょう)』には「式を用いる法は、朝は南を向き、暮は北を向き、
常に左手を以って鬼門を執り、右手をもて月将を転ず」とある。(文献1③、6①)
つまり式盤で占うときには、地盤の鬼門(北東:艮(うしとら):丑と寅の間)が左手にくるように使うため、午(南)の方位が上になる。
この天文学的理由は式盤を星座早見盤化することにより後程明らかにされる。
<占い方>
占い方の詳細については文献5と6を参照願いたい。
文献5はコンパクトな解説書で、占いのための計算ソフトが添付されている。
文献6は大部な専門書で『占事略决』の本格的な研究書である。
ここでは、天文学的な解明が目的であることから、ごく簡単に紹介しておく。
占いは、占う時刻(占時)からスタートする。
該当する月の月将を選定し、天盤にあるその月将を地盤の時刻(十二支)にあわせる。
月将は十二神古名とも呼ばれ、月との対応は下記の通りである。
微明(びめい)(正月)、魁(かい)(二月)、従魁(じゅかい)(三月)、伝送(でんそう)(四月)、
小吉(しょうきち)(五月)、勝光(しょうこう)(六月)、太一(たいいつ)(七月)、天閏(てんじゅん)(八月)、
太衝(たいしょう)(九月)、功曹(こうそう)(十月)、大吉(だいきち)(十一月)、神後(しんこう)(十二月)
初期条件を図4の天盤の神後(しんこう)と地盤の子が一致の状態として、
ここから天盤の動いた左回りの角度を30°で除した0~11の整数が引数(ひきすう)となる。(十二支は30°ステップ)
例えば、12月の午後6時であれば、天盤の十二月の神名である神後を地盤の酉の刻にあわせればよい。
この時の移動角度は左回りに90°であるから、引数は3となる。
引数は天盤の移動のない0を含めて12通りある。
それに日の干支をからめて占いを行う。
ここで注目すべきは、月将を占時に合わせる行為である。
これは、二次元平面における星空の回転運動を表しており、その機能は現在の星座早見盤と本質的に同じである。
天盤の二十八宿と月将は、星と黄道上の太陽の関係に置き換えられる。
これは、次に述べる星座早見盤の黄道の描かれた星空と月日が刻まれた星座盤に相当する。(図5参照)
また、地盤の時刻と方位は、星座早見盤の地平盤に相当する。
そのため式盤の天文学的解明には、星座早見盤の検討が出発点となる。
3 星座早見盤の基本原理
星は地下から登り、地下へと沈んでゆく。
これを2枚の盤で表現するならば、星座が描かれた星座盤と地平面が描かれた地平盤となる。
構造的には、星座盤の上に地平盤が置かれる。
視太陽時の場合、原理的には黄道上の太陽に子午線を重ねるだけのことである。
太陽は黄道上を一年で回るので、太陽の位置は暦となる。
現用の平均太陽時(UT1)の場合は、天の赤道を等速運動する平均太陽の赤経に対応させた暦となる。
この月日の詳細を表示したものが、図5の星座早見盤外周の月日目盛である。

図5 傘差し型星座早見盤 現在の星座早見盤(北緯35°・東経135°兵庫県立西はりま天文台監修)
星座盤:下の金属の皿、外周の月日の目盛は右回り。
地平盤:上のセルロイドのカバー、時刻目盛は左回り。
東南西北の表記順が左回りとなっていることに注目。
地平面は窓の外の白い部分にあたる。
今、この月日目盛(平均太陽の位置)に地平盤の南側の子午線を合わせれば、その月日の12時(正午)の星空が表示される。
原理的には、これを1時間に15°の割合で星座盤を左回転させれば求める星空が得られる。
これは、地平盤を右回転させることと同じでことである。
実際の使用に当たっては、地平盤の時刻目盛を所定の月日目盛に合わせるだけで良い。
現在の星座早見盤は、傘を差すように地平盤の天頂を頭上に置き、窓の外周の方位に合わせて星空を観察するものである。
傘の石突きにあたる星座盤の回転軸を地平線上の北極星に合わせれば天頂が頭上にくるので、
私は現在の星座早見盤を傘差し型星座早見盤と呼んでいる。
一方、六壬式盤は据置いて使用するものであるから据置き型星座早見盤と呼んでいる。
<六壬式盤との比較検討>
ここで図4の六壬式盤と図5の星座早見盤を比較しよう。
最初に、注目したいのは方位の回転方向である。
基準となる方位の文字列を「東南西北」(式盤では「卯午酉子」)とする時、
六壬式盤の文字列の回転方向は、右回りとなっていて地上の方位と同じである。
一方、星座早見盤は、それが図5のように左回りとなる。
星座早見盤の方位は、天の北極を見上げた時のものである。
だとしたら、六壬式盤の方位は天の南極を見下ろした時のものとなる。
次に、基準となる二十八宿の文字列を
「角亢氐房心尾箕斗牛女虚危室壁奎婁胃昴畢觜参井鬼柳星張翼軫」とするとき
星座早見盤の文字列の回転方向は右回りとなり、据置き型星座早見盤は左回りとなる。
宋代の蘇頌(そしょう)の『新儀象法要』に、渾象に描いた星を平面図に展開した挿図がある。(HP3)
図6はその一部で、図6Aは天の北極、図6Bは天の南極を中心とした星図である。
図6の外周には、角から軫の二十八宿が記載されていて、その表記順は北極図が右回りで南極図が左回りとなっている。
尚、南極図の中央の白い円は、地平面の下に隠れた天の南極の外規を表現している。
これを図4の六壬式盤と図5の星座早見盤を対比させれば、その基本概念は図6Aに図5、図6Bに図4が対応していることがわかる。
実際に二十八宿の回転運動を確認しようとして図5の星座早見盤を動かしてみると、
南の星空の視覚的な再現性が極めて乏しいことに気づくだろう。
これを克服するには星座盤をドーム状にする必要があり、二次元平面における表現形態からは逸脱する。
図5の星座早見盤の外周が内側に湾曲しているのはそのためである。
天の北極を回転の中心とした星座早見盤は、南の空の観察には不向きなのである。
二十八宿は天の赤道付近に位置するため南の空に展開する。(図7B参照)
そのため、天の南極を回転の中心とした据置き型星座早見盤の作成が次の課題となる。
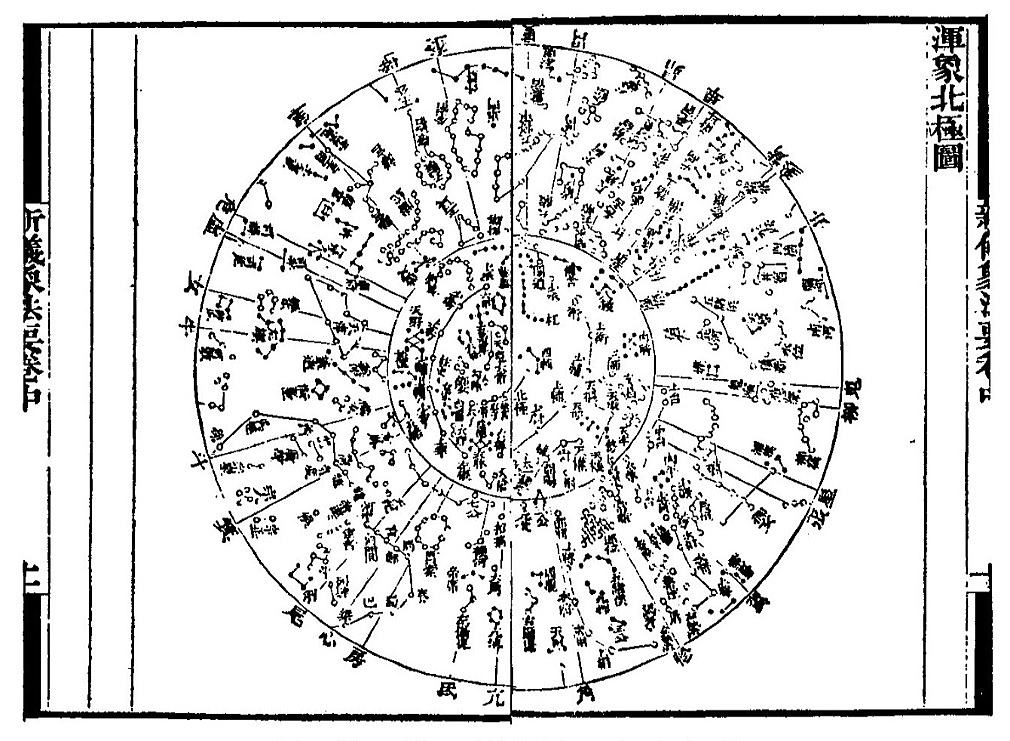
図6A 蘇頌の星図 渾象北極図 二十八宿(角~軫)の表記順は右回り(文献8) 傘差し型星座早見盤(図5)に対応
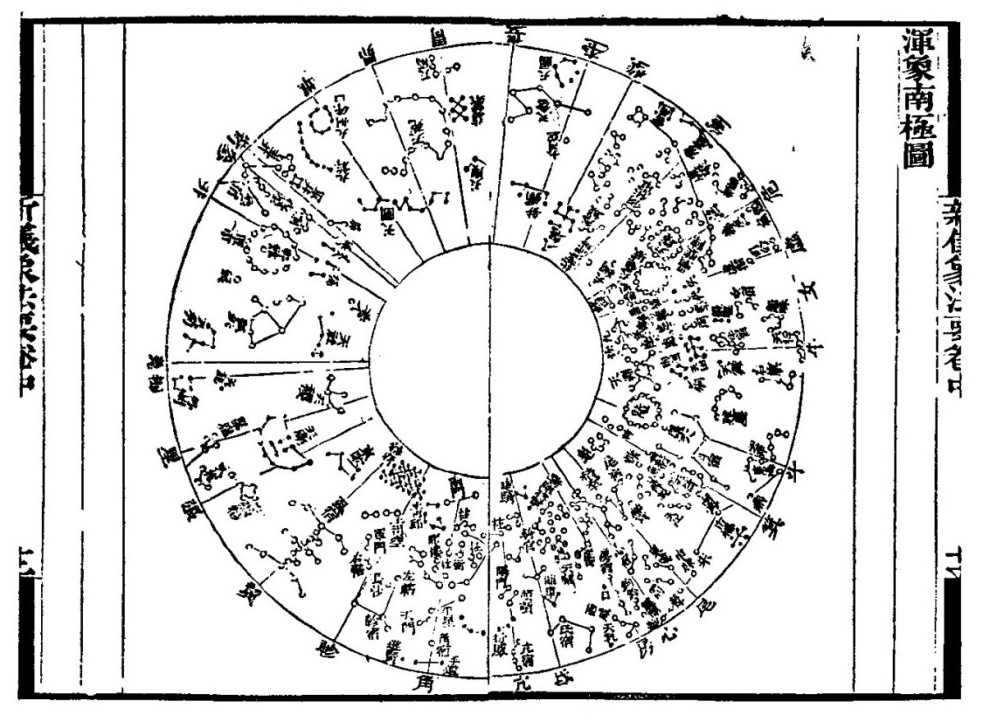
図6B 蘇頌の星図 渾象南極図 二十八宿(角~軫)の表記順は左回り(文献8) 据置き型星座早見盤(図4)に対応
4 据置き型二十八宿早見盤の設計
六壬式盤を星座早見盤と仮定するならば、それは原理的には現在の星座早見盤の回転軸を天の南極に切り替えたものとなる。
<作成要領>
地域:中国阜陽(ふよう)市 北緯32.9°東経115.8°
年代:紀元前172年 二十八宿の距星の赤経α,赤緯δ(表1参照)
星座盤
天の南極を中心とした正距方位図法で表現 対蹠地(たいせきち)は天の北極
天の赤道の半径を球面三角法により90°と定める。
立春点を基点にして、二十八宿の表記順を左回りとする。
星の座標(赤経α,赤緯δ)の表示
x= (90+δ) ・ sinα y=- (90+δ) ・cosα (1)
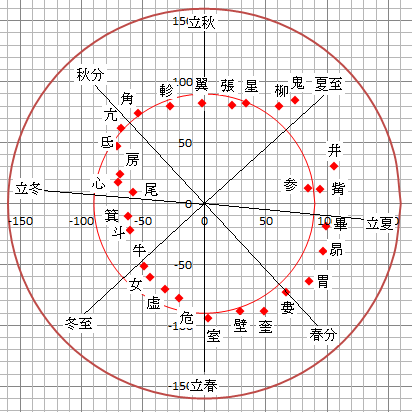
図7A 星座盤の設計 中央の円は天の赤道 赤緯はプラスが外側、マイナスが内側
春分線が婁宿(赤経0.06°)を貫いている。(表1参照)
表1 紀元前172年3月24日春分の二十八宿の赤経と赤緯
| 星宿名 | 距星 | 赤経α | 赤緯δ | ||||||
| h | m | s | α° | 度 | 分 | 秒 | δ° | ||
| 1 角(かく) | αVir | 11 | 33 | 49.9 | 173.46 | 0 | 46 | 50 | 0.78 |
| 2 亢(こう) | κVir | 12 | 20 | 43.1 | 185.18 | 1 | 5 | 8 | 1.09 |
| 3 ?(てい) | αLib | 12 | 55 | 53.9 | 193.97 | -5 | -24 | -39 | -5.41 |
| 4 房(ぼう) | πSco | 13 | 54 | 32.7 | 208.64 | -17 | -27 | -8 | -17.45 |
| 5 心(しん) | σSco | 14 | 15 | 42 | 213.93 | -17 | -45 | -57 | -17.77 |
| 6 尾(び) | μSco | 14 | 33 | 27.5 | 218.36 | -31 | -13 | -3 | -31.22 |
| 7 箕(き) | γSgr | 15 | 49 | 34.4 | 237.39 | -27 | -3 | -55 | -27.07 |
| 8 斗(と) | φSgr | 16 | 30 | 44.6 | 247.69 | -25 | -49 | -54 | -25.83 |
| 9 牛(ぎゅう) | βCap | 18 | 16 | 13.5 | 274.06 | -18 | -50 | -19 | -18.84 |
| 10 女(じょ) | εAqr | 18 | 47 | 21.5 | 281.84 | -14 | -55 | -9 | -14.92 |
| 11 虚(きょ) | βAqr | 19 | 34 | 21.7 | 293.59 | -13 | -1 | -13 | -13.02 |
| 12 危(き) | αAqr | 20 | 12 | 5.3 | 303.02 | -9 | -9 | -3 | -9.15 |
| 13 室(しつ) | αPeg | 21 | 17 | 31.5 | 319.38 | 4 | 31 | 59 | 4.53 |
| 14 壁(へき) | γPeg | 22 | 23 | 42.4 | 335.93 | 3 | 21 | 36 | 3.36 |
| 15 奎(けい) | ζAnd | 23 | 6 | 9.6 | 346.54 | 11 | 23 | 33 | 11.39 |
| 16 婁(ろう) | βAri | 0 | 0 | 15.4 | 0.06 | 9 | 13 | 4 | 9.22 |
| 17 胃(い) | 35Ari | 0 | 43 | 52 | 10.97 | 16 | 52 | 42 | 16.88 |
| 18 昴(ぼう) | 17Tau | 1 | 42 | 38 | 25.66 | 15 | 2 | 1 | 15.03 |
| 29 畢(ひつ) | εTau | 2 | 26 | 53.9 | 36.72 | 11 | 45 | 31 | 11.76 |
| 20 觜(し) | λOri | 3 | 38 | 2.3 | 54.51 | 5 | 37 | 56 | 5.63 |
| 21 参(しん) | δOri | 3 | 42 | 58.9 | 55.75 | -4 | -33 | -31 | -4.56 |
| 22 井(せい) | μGem | 4 | 13 | 12.8 | 63.30 | 20 | 22 | 16 | 20.37 |
| 23 鬼(き) | θCnc | 6 | 24 | 3.8 | 96.02 | 22 | 35 | 58 | 22.60 |
| 24 柳(りゅう) | δHya | 6 | 40 | 23.8 | 100.10 | 10 | 44 | 44 | 10.75 |
| 25 星(せい) | αHya | 7 | 39 | 58.4 | 114.99 | -1 | -11 | -40 | -1.19 |
| 26 張(ちょう) | υHya | 8 | 6 | 58.9 | 121.75 | -6 | -21 | -58 | -6.37 |
| 27 翼(よく) | αCrt | 9 | 14 | 9 | 138.54 | -7 | -42 | -22 | -7.71 |
| 28 軫(しん) | γCrv | 10 | 26 | 57 | 156.74 | -5 | -42 | -13 | -5.70 |
地平盤
図7Bにおいて、時角Hは天の北極と天頂を結ぶ線を基準にして時計回りとする。
天の北極・天頂・天体を頂点とする球面三角形(斜線で示した部分)に、余弦定理と正弦余弦定理を適用して (2)式と(3) 式を得る。
sinδ= sinφ・sin h+cosφ・cos h・cos A (2)
cos H=( cosφ・sin h-sinφ・cos h・cos A) / cosδ (3)
地平線・方位線・等高線は、(2)式より赤緯δ、(3) 式より時角 Hを求めて、下式によりグラフを描くことができる。
地平線(h=0°) tanδ=-cos H / tanφ (4)
子午線上(A=180° H=0°) y=φ+h (5)
x= (90+δ) ・ sin H y= (90+δ) ・cos H (6)
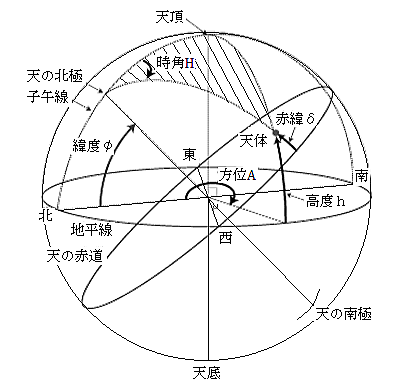
図7B 地平座標系と赤道座標系
緯度φ・方位A・高度h・赤緯δ・時角 H
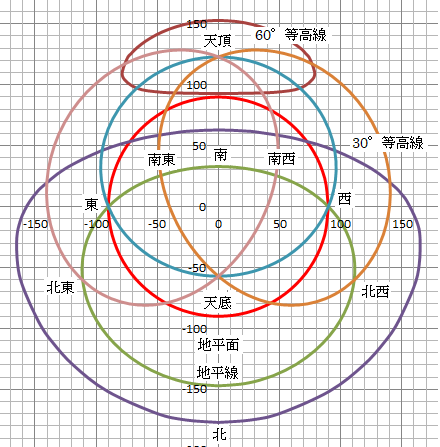
図7C 地平盤の設計 地平線・方位線・等高線・天の赤道の概念図
図7Cには二つの極がある。一つは地面の上(天頂)にあり、もう一つは地面の下(天底)にある。(図7B参照)
東西線と地平線と天の赤道はx軸上にある東西の一点で交わる。
図7Dは、図7Aと図7Cを組み合わせた据置き型二十八宿早見盤である。
図7Dの二十八宿早見盤と図5の星座早見盤を比較すると、地平線を境界として天地が反転していることがわかる。
地平面は天頂と天底を両極とする天球を二分し、その南北間の距離は180°である。
南側の子午線上の地平線の位置は緯度φに等しく、天頂はφ+90°となる。
等高線は、h<φの時は地平面を囲い、h>φの時は天頂を囲う。
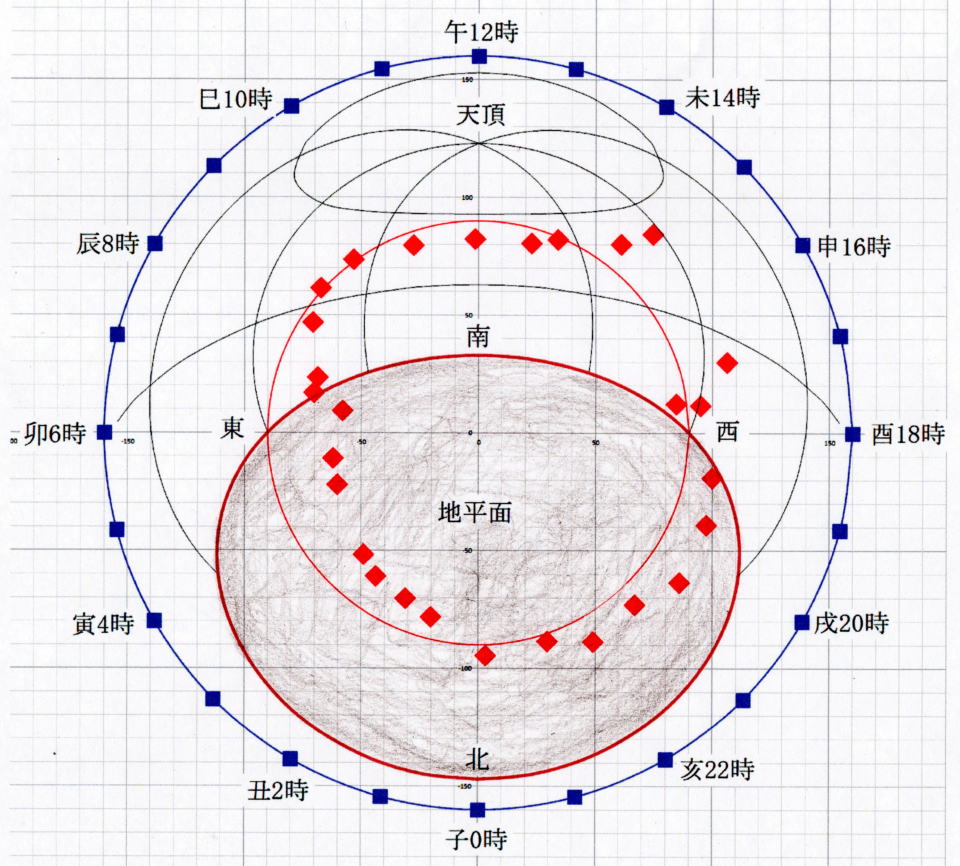
図7D 据置き型二十八宿早見盤(図7Aと図7Cを組み合わせたもの)
紀元前172年2月6日(立春)の午前0時の星空(星宿の詳細は図7A参照)
5 前漢汝陰侯墓出土の六壬式盤 午前0時に展開する二十八宿
図8は、現在最古のものとされる前漢汝陰侯墓出土六壬式盤(図1)の解説図である。
天盤の中央に裏向きに描かれた北斗七星、周りには左回りに二十八宿が描かれ、
そのうちの十二宿に正から十二までの数字が付記されている。
これは後に月将と呼ばれる正月から十二月までの月を表している。
天盤は二十八宿が均等に配置されている。
地盤は三つの区域に分けられ、天盤のすぐ外の区域は十干が東の甲乙にはじまって右回りに丙丁・庚辛・壬癸と書きこまれている。
そして、北西には「天豦己」、南東には「土斗戊」、南西には「入日己」、北東には「鬼月戊」と書かれている。
これは後の天門・地戸・人門・鬼門にあたる。
さらにその外側には、十二支が四方に三つずつ、北方の亥・子・丑からはじまって右回りに描かれる。
そして、外周には二十八宿が東方の角から左回りに書きこまれている。
ここで注目したいことは、四維(しい)に書き込まれた「天豦己」の文字である。
「天(てん)豦(きょ)己(き)」の天は天門であるが、豦(きょ)はわかりにくい。
しかし、漢和辞典(文献9)で調べて行くと
豦(きょ)→豕(し)・豕韋(しい)→營室(えいしつ)とつながり、二十八宿の室宿であることがわかった。
『春秋左氏伝』昭公十一年(BC531年)春の記述にも「歳在豕韋」とある。(文献10)
室宿が立春正月を告げる顓頊暦(せんぎょくれき)における重要な宿であったことがわかる。(文献11)
ここで、図4武威磨咀子(ぶいまそし)三座漢墓と図8汝陰侯墓の式盤を比較して見ると、
武威磨咀子三座漢墓の月を表す神名が30°等間隔に配置されているのに対し、
汝陰侯墓の式盤の正月から十二月までの月は均等に配置されていないことがわかる。
それゆえ、この暦の正体の解明が次の課題となる。
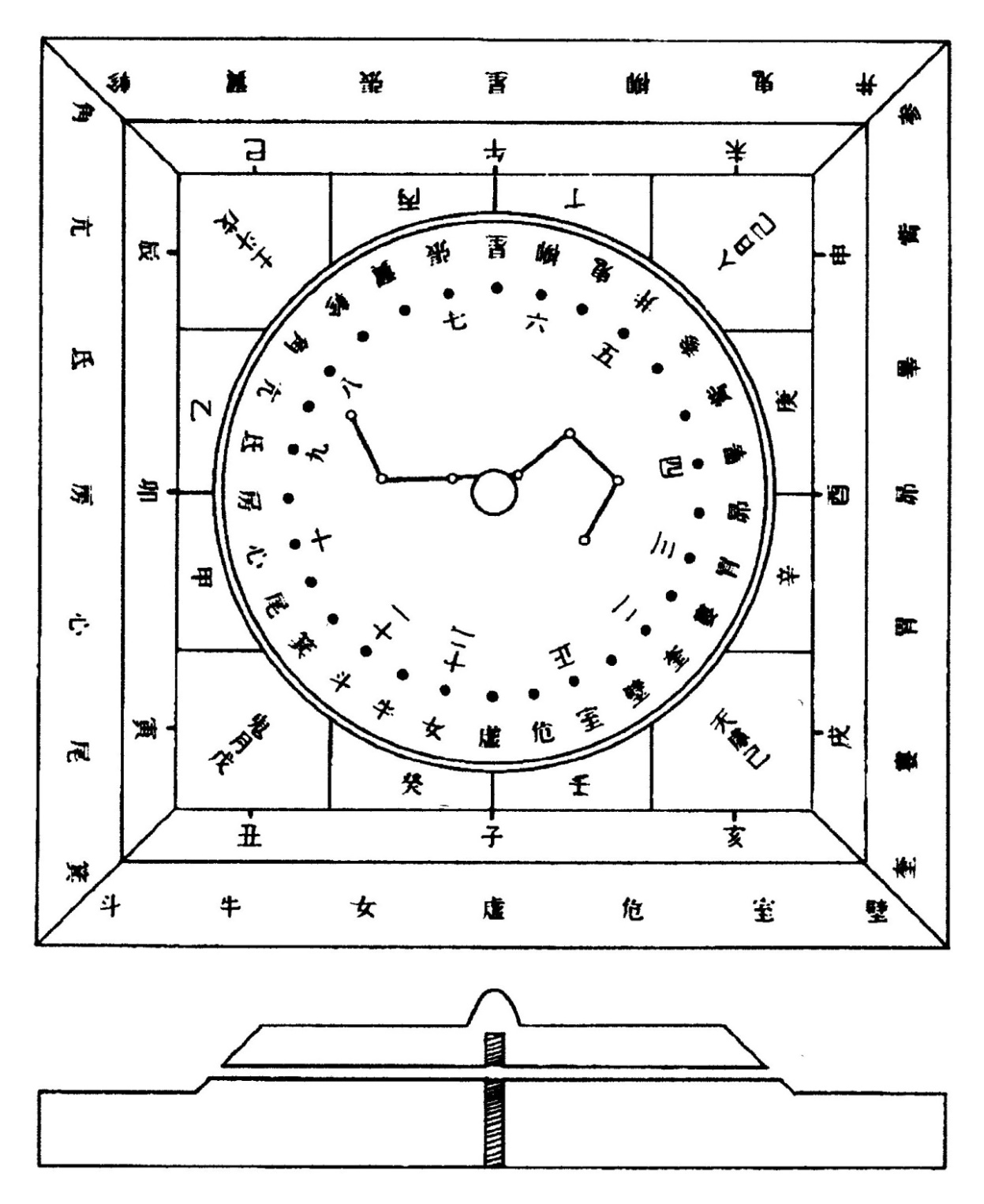
図8 前漢汝陰侯墓出土六壬式盤の解説図(文献1④) 出土遺物の原図は図1参照
<太乙九宮占盤 六壬式盤の暦>
上記に関連して、前述の汝陰侯墓同時出土の太乙九宮占盤(たいいつきゅうきゅうせんばん)(図2)がある。
これは呼び名が示す通り占具であるが、占い方の解説については文献1⑤を参照願いたい。
ここでは裏面に記載された「七年辛酉(しんゆう)日中冬至」の文字と八節の間隔を示す日数に着目したい。
表2は、これを天文ソフトと比較したものである。
通日は、古代中国の暦の伝統に従い、太乙九宮占盤の文帝七年(BC173年)冬至の日を起算日としている。
表2 八節の日数(BC173年冬至~BC172年冬至)
上段:冬至側(近日点) 下段:夏至側(遠日点) 通日:冬至第1日
|
|
秋分 |
→ |
立冬 |
→ |
冬至 |
→ |
立春 |
→ |
春分 |
合計 |
|
太乙九宮占盤 |
|
45 |
|
45 |
|
46 |
|
46 |
|
182 |
|
通日 |
276 |
|
321 |
|
1 |
|
47 |
|
93 |
|
|
天文ソフト |
|
45 |
|
44 |
|
44 |
|
46 |
|
179 |
|
通日 |
277 |
|
322 |
|
1 |
|
45 |
|
91 |
|
|
|
春分 |
→ |
立夏 |
→ |
夏至 |
→ |
立秋 |
→ |
秋分 |
合計 |
|
太乙九宮占盤 |
|
46 |
|
45 |
|
46 |
|
46 |
|
183 |
|
通日 |
93 |
|
139 |
|
184 |
|
230 |
|
276 |
|
|
天文ソフト |
|
47 |
|
47 |
|
47 |
|
45 |
|
186 |
|
通日 |
91 |
|
138 |
|
185 |
|
232 |
|
277 |
|
天文ソフトによれば、近日点のある冬至側は日数が夏至側より7日短くなっている。
それに対し、九宮盤の両者はほぼ等しく、また八節の間隔が45日と46日の組合せであることから明らかに平気法であることがわかる。
六壬式盤の暦は太陽暦でなければならないから節月であると考えられる。(文献12)
陰陽道においても、節気により月を区切る方法が用いられている。(文献6②)
そこで、九宮盤の表2のデータから前漢の暦法に従って冬至起算の平気法に準拠した式盤用の暦をここで作成する。
まず表2の九宮盤の八節の間隔を合わせこんだ節月の暦を作成するために1年365日を、30日と31日の月で次のように構成する。
30日の月 二月 四月 五月 八月 九月 十月 十二月
31日の月 正月 三月 六月 七月 十一月
正月一日は冬至から数えて47日目(立春から2日遅れ)の日となる。
月の中間の日付は分割のない月が一日、2分割が一日・十六日、3分割が一日・十一日・二十一日とする。
表3にその結果を示す。表2の八節の間隔は表3とぴったり一致していることがわかる。
尚、表3の通日は表2に示されるように、数学的には巡回群であるから365を法とする合同式で表される。
例えば、表3の式盤の十二月十一日の通日は、BC173年の冬至から数えて392日目であるが、これから365日を減じて27日とする。
| 表3 前漢汝陰侯墓出土六壬式盤の暦と二十四節気(BC173年12月~BC171年1月) |
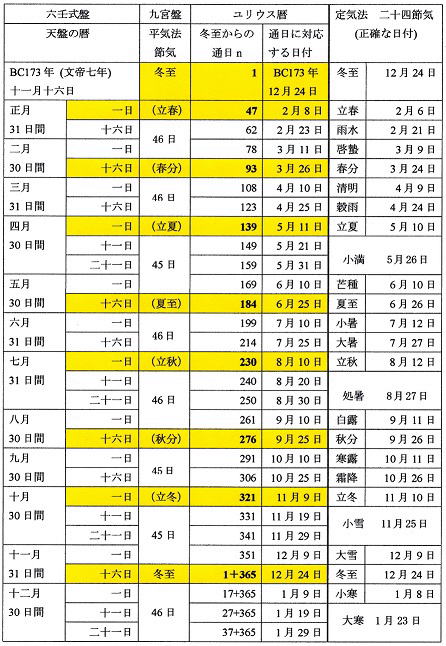 |
| (注)九宮盤の二十四節気は平気法によるもので、現実とは約±2日のズレがある。 |
表3の暦が出来上がったところで、正月一日の午前0時の星空を眺めてみよう。
古代中国の時制では、午前0時は夜半と呼ばれ一日の始まりとされている。
それには、図7D据置き型二十八宿早見盤の要領に従って、図8の地盤の子の位置に正月一日(室宿の位置)を合わせる。
図7D据置き型二十八宿早見盤を見ると、地平線は東西線(卯酉(ぼうゆう)線)のやや北寄りに垂れていることがわかる。
このことから、図8の式盤の夜空に展開する二十八宿は觜参井鬼柳星張翼軫角亢氐房心尾の15宿となる。
これを図7D据置き型二十八宿早見盤で確認すると觜参井鬼柳星張翼軫角亢氐房心(図7A参照)となり、
最後の尾を除いて完全に一致していることがわかる。
尾は赤緯がマイナスに大きく振れているので地下にある。(図7A、7D参照)
図9Aは、これをステラナビゲータの地平座標形式:BC172年2月8日(正月一日)の午前0時(視太陽時)で検証したものである。
これは、図7D据置き型二十八宿早見盤の立春の日から2日遅れの二十八宿に相当する。
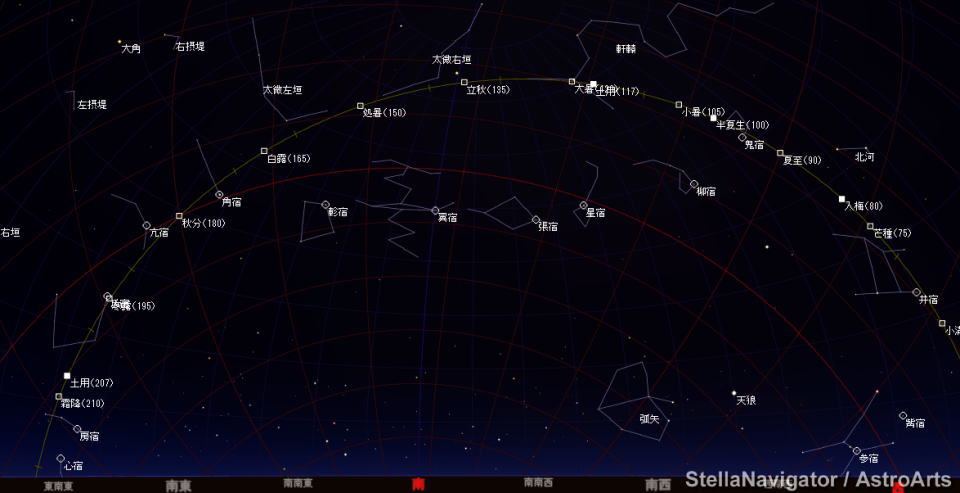
図9A BC172年2月8日(正月一日)の午前0時(視太陽時)の星空
觜参井鬼柳星張翼軫角亢氐房心の宿が南の空に展開している。
次に、図8の正月十六日(壁宿の位置)を子の位置におくと
式盤の夜空に展開する二十八宿は参井鬼柳星張翼軫角亢氐房心尾箕となり、星宿は一つ移動する。
式盤上に展開する二十八宿は常に卯酉線から上の15宿である。
尚ここで、月日の下の二十八宿は必ずしもヘリアカルライジングを意味するものでないことに留意されたい。
これを、天文ソフトのBC172年2月23日(正月十六日)の午前0時で確認すると、井鬼柳星張翼軫角亢氐房心尾となり、
参と箕の両端を除いて式盤で求められたものと一致していることがわかる。
さらに正月一日から半年後の七月一日(BC172年8月10日)午前0時の星空は斗牛女虚危室壁奎婁胃昴畢となり、
西方の心尾箕を除いて式盤で求められたものと一致していることがわかる。(図9B参照)
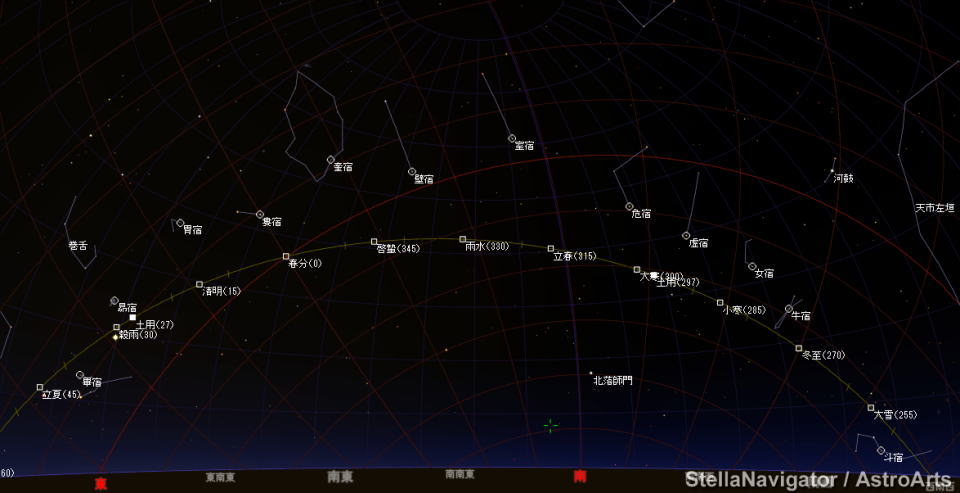
図9B BC172年8月10日(七月一日)の午前0時(視太陽時)の星空
斗牛女虚危室壁奎婁胃昴畢の宿が南の空に展開している。
この手順を全面展開したものが表4である。
表4は、図8の天盤を回転させることによって求められた二十八宿と表3の通日から天文ソフトで求められた二十八宿を比較したものである。
[ ~ ]の階段状に変化するのが式盤から機械的に求められる二十八宿で、白地の部分が天文ソフトから求められた二十八宿である。
黒地の部分は地下を意味する。
地平線近くの星宿はズレているものもあるが、この種のものとしては素晴らしい出来栄えと言えよう。
表4 前漢汝陰侯墓出土六壬式盤に表示される午前0時の二十八宿
天文ソフト :白地に表記された二十八宿(黒マーカーは地下の二十八宿を示す)(七月十一日の井宿を除いて連続)
六壬式盤 :白地の二十八宿を含む [ ~ ] 間の範囲(連続)
二十八宿円盤 :白地の七宿以上の二十八宿を含む四角の囲み文字間の範囲(連続)

6 前漢汝陰侯墓出土の二十八宿円盤 六壬式盤のデータ源
次に問題となるのは六壬式盤の設計がなにをもとにおこなわれたかということである。
図10は前漢汝陰侯墓から六壬式盤と同時に出土した二十八宿円盤(図3)の解説図である。
上盤には中央に回転軸の通る穴と、外周に365個の度数と言われている点(小孔)がある。(HP4参照)
二十八宿の配置が実際のものに近いことから、これは天文観測器具と考えられている。
これをずばり星座早見盤であると言ったら驚くであろうか。
なぜなら、星座盤にあるはずの月日目盛もなく、地平盤にあるはずの時刻目盛もないからである。(図5参照)
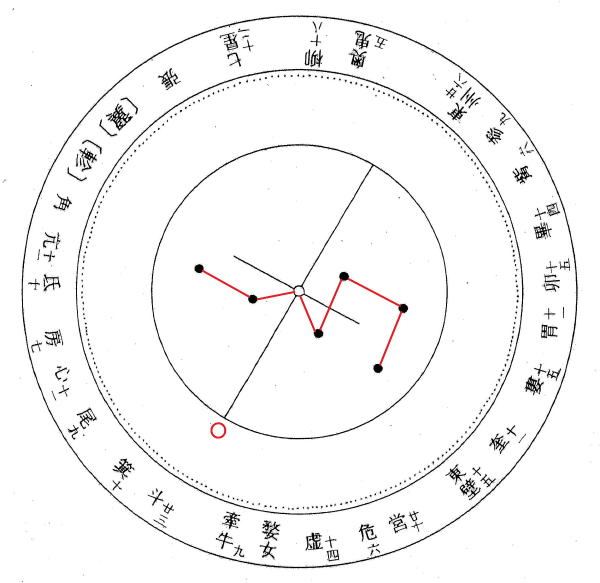
図10 前漢汝陰侯墓出土の二十八宿円盤(解説図) 出土遺物の原図は図3参照
各二十八宿名のそばには、度数が記載されている。
本図は解説のため、上盤と下盤の比率を大きく変えてある。(文献1⑥)
北斗七星を結ぶ線と〇印は、筆者が追記(詳細本文参照)
<二十八宿早見盤の設計 通日度数nと赤経度数m>
設計にあたって、まず図7Dと図10を比較する。
星座早見盤の基本原理のところでも述べたように、星座盤に上にあるものは地平盤であるから、図10の上盤は地平盤である。
ここで二十八宿の回転を、365を法とする合同式で表現するために、
上盤の365個の打点に表3の冬至からの通日に対応する度数としてn=1~365の番号を右回りに付与する。(図11参照)
この時、正月一日の通日n=47を長い方の線分の下に置く。
次に、下盤の二十八宿の赤経に対応する度数としてmを左回りに付与する。
この赤経度数mは、360°で一巡する赤道座標を365度(中国度)で一巡する度数で置き換えたものである。
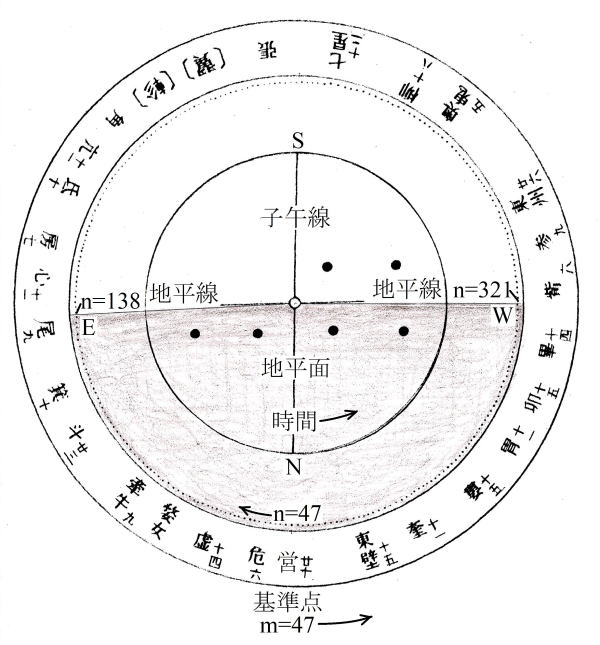
図11 二十八宿円盤における二十八宿早見盤の設計図(図7D参照)
n:通日度数(右回り) m:赤経度数(左回り) 星空の可視範囲n=138~321
正月一日:通日n=47 基準点:室宿m=47
二十八宿の度数は、各二十八宿の間隔を度数で示したものであるから、赤道座標に固定する必要がある。
固定方法の一つは、12時(正午)に南中する宿を赤道座標の基準点とすることである。
ここで、前述の太乙九宮占盤に書き込まれた「天(てん)豦(きょ)己(き)」の銘を思い起こすならば、
正月一日と室宿の緊密な関係が予想できる。
戦国末の成立とされる『呂氏春秋』十二紀 正月紀にも、「孟春之月:日在營室,昏參中,旦尾中。」とある。(HP5)
孟春とは春の始まりであり正月のことである。営宿(室宿)は太陽とともにあり、夕方に参宿が南中し、朝方に尾宿が南中するとある。
天文ソフトによれば、それを裏付けるかのようにその日に正午に室宿が南中していることが確認できる。
天文データ:正月一日(BC172年2月8日 通日n=47)
・正午(視太陽時)における室宿の方位:南を0°として東に0.5°
・参宿南中:18時25分22秒(視太陽時) 日没後1時間03分00秒
・尾宿南中:05時17分58秒(視太陽時) 日出前1時間20分02秒
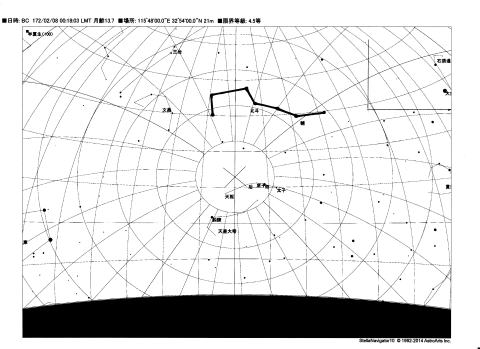
ここで、改めて正月一日午前0時の北斗七星を天文ソフトで確認すると、
北斗七星の柄の方向は真東を指していることがわかる。(図12参照)
 |
||
| 西(酉) | 北(子) | 東(卯) |
図12 正月一日(BC172年2月8日)の午前0時(視太陽時)の北斗七星
北斗七星の柄が東を向き、子午線と直交していることに注目
北斗七星の柄は斗建と呼ばれ、季節・時刻・方位を示すものとして古来より重視されてきた。
このことから前述の「通日n=47を長い方の線分の下の置く」とは、
北斗七星との配置を考慮するならば図10の下側(〇印)であることがわかる。
また図11の地平線と子午線の方位(S,N)との関係も留意すべきである。
天文ソフトの北斗七星(図12)と宿盤の北斗七星(図10)を比較すると、
宿盤の北斗七星は左右を反転させて裏向けに描かれていることがわかる。
図1の前漢汝陰侯墓出土六壬式盤の北斗七星と同様である。
これは、天の北極を通して天の南極を見下ろした図で、図6B蘇頌の星図「渾象南極図」に対応するものであり、
天の南極を表象するものであろう。
表5に様々な資料と計算値をもとに室宿をm=47に設定した二十八宿の赤経度数mを示す。
隣合うmの差は二十八宿の度数である。
表5 二十八宿の赤経度数mと二十八宿の見える範囲
m=((n+91)~(n+274)) (mod365) n冬至からの通日
|
星宿名 |
二十八宿の古度 |
赤経度数m |
|||||
|
宿盤Ⅰ |
宿盤Ⅱ |
洪範 |
漢書 |
計算値 |
採用値 |
採用値 |
|
|
1 角(かく) |
不明 |
不明 |
12 |
12 |
11.9
|
12 |
274 |
|
2 亢(こう) |
11 |
11 |
不明 |
9 |
8.9
|
11 |
286 |
|
3 氐(てい) |
10 |
1? |
17 |
15 |
14.9
|
17 |
297 |
|
4 房(ぼう) |
7 |
7 |
7 |
5 |
5.4
|
7 |
314 |
|
5 心(しん) |
11 |
11 |
12 |
5 |
4.5
|
11 |
321 |
|
6 尾(び) |
9 |
9 |
9 |
18 |
19.3
|
9 |
332 |
|
7 箕(き) |
10 |
10 |
10 |
11 |
10.4
|
10 |
341 |
|
8 斗(と) |
23 |
22 |
22 |
26 |
26.7
|
22 |
351 |
|
9 牛(ぎゅう) |
9 |
9 |
9 |
8 |
7.9
|
9 |
8 |
|
10 女(じょ) |
不明 |
10 |
10 |
12 |
11.9
|
10 |
17 |
|
11 虚(きょ) |
14 |
14 |
14 |
10 |
9.6
|
14 |
27 |
|
12 危(き) |
6 |
6 |
9 |
17 |
16.6
|
6 |
41 |
|
13 室(しつ) |
20 |
20 |
20 |
16 |
16.8
|
20 |
47 |
|
14 壁(へき) |
15 |
15 |
15 |
9 |
10.8
|
15 |
67 |
|
15 奎(けい) |
11 |
11 |
12 |
16 |
13.7
|
11 |
82 |
|
16 婁(ろう) |
15 |
15 |
15 |
12 |
11.1
|
15 |
93 |
|
17 胃(い) |
11 |
11 |
11 |
14 |
14.9
|
11 |
108 |
|
18 昴(ぼう) |
15 |
15 |
15 |
11 |
11.2
|
15 |
119 |
|
19 畢(ひつ) |
14 |
15 |
15 |
16 |
18.0
|
15 |
134 |
|
20 觜(し) |
6 |
6 |
6 |
2 |
1.3
|
6 |
149 |
|
21 参(しん) |
9 |
9 |
10 |
9 |
7.7
|
9 |
155 |
|
22 井(せい) |
26 |
26 |
29 |
33 |
33.2
|
26 |
164 |
|
23 鬼(き) |
5 |
5 |
5 |
4 |
4.1
|
5 |
190 |
|
24 柳(りゅう) |
18 |
18 |
18 |
15 |
15.1
|
18 |
195 |
|
25 星(せい) |
12 |
12 |
13 |
7 |
6.8
|
12 |
213 |
|
26 張(ちょう) |
不明 |
不明 |
13 |
18 |
17.0
|
16 |
225 |
|
27 翼(よく) |
不明 |
不明 |
13 |
18 |
18.5
|
17 |
241 |
|
28 軫(しん) |
不明 |
不明 |
16 |
17 |
17.0
|
16 |
258 |
|
合計 |
- |
- |
- |
365 |
365.0 |
365 |
- |
(注)宿盤Ⅱ:氐 10の下一桁不明 赤経度数mは室宿m=47を基準として算出
<表5の出典>
宿盤Ⅰ:「西漢汝陰侯墓出土的占盤和天文円儀」殷涤非(いんじょうひ) 『考古』 1978年5期 339
宿盤Ⅱ:「我國早期的二十八宿觀測及其時代考」潘鼐(はんだい) 『中華文史論叢』1979年第3輯(總第11輯) 163~164
洪範:劉向『洪範伝(洪範五行伝)』(『開元占経』所引)
「開元占経:巻60~63 中國哲學書電子化計劃」https://ctext.org/wiki.pl?if=gb&chapter=783001
漢書:「漢書:志:律暦志139 中國哲學書電子化計劃」https://ctext.org/han-shu/lv-li-zhi/zh
表5の宿盤Ⅰは発掘の翌年の調査報告、宿盤Ⅱはさらにその1年後のかなり詳細な論文で、厳密な検討がなされているものと想定される。
洪範とあるのは、『開元占経』に古度とあるもので、多くの文献に比較的宿盤の度数と合っているものとして紹介されている。
漢書は、二十八宿の度数を最も一般的に代表するものである。
二十八宿の古度の計算値は、表1の隣合う二十八宿の赤経差(°)を、(365/360)倍して中国度数に換算したものである。
また、古度の採用値は、宿盤Ⅱをベースとして、不明のところは洪範と計算値等を勘案したものである。
現実の太陽の運行を精密に宿盤の動きで表現することは不可能であるから、
ここでは古代中国の暦法(文献13)に従って天の赤道を1日1度で等速運動する太陽を想定する。
これを日行一日一度と称している。そうすると、星の出は1日1度の割合で早くなる。
今、通日度数nを表2、3の太乙九宮占盤における冬至からの通日とする。
ここで冬至点を赤経度数m=1と置くならば、日行一日一度により室宿のmは表2よりm=47となる。
正月一日の通日n=47を表5の室宿の赤経度数m=47に合わせると、その合計はn+m=94となる。
回転の向きが逆なので、他の相対するmとnの間に下式が成立する。(図11参照)
94≡(m+n) (mod365) (7)
一般に、m=kmにn=knを合わせる時、下式となる。
(km+kn)≡(m+n) (mod365) (8)
図11は図7Dから得られた二十八宿早見盤の設計図である。
地下の子午線(N側)の下にある宿は正午に南中する宿である。
地平線は六壬式盤の例にならい、nが137と138、321と322の間に設けた。
これにより地平線は水平よりも0.74°わずかに垂れる形となり、星空の可視範囲はn=138~321となる。
可視範囲の中央値n=229.5が南の子午線の位置である。
図5の星座早見盤の動きをみると、地球の日付盛りに表される年周運動と時刻目盛に表される日周運動に分けられる。
ここでは、それに従って数式化を試みる。尚、日周運動は次の「二十八宿円盤における合同式の一般化と精度」のところで述べる。
年周運動
まずは正月一日(通日47日)の午前0時の星空を求めよう。
それには地下の子午線の下にあるn=47を基準点(室宿m=47)に合わせれば良い。
そうすると、星空の可視範囲は、n=138~321(図11参照)であるからmは(7)式よりm=138~321となる。
従って、表5より南の空に展開する二十八宿は「觜参井鬼柳星張翼軫角亢氐房心」であることがわかる。
また(8)式より通日nを基準点(m=47)に合わせた時の地下の子午線(n=47)に合わさる赤経度数mはnに等しく、
任意の二十八宿が正午に南中する通日nはその宿のmとなる。
次に、正月二日(通日48日)の午前0時の星空を求めよう。
星座盤のかわりに上盤(地平盤)のn=48(通日48日)を基準点(室宿m=47)に移動すると、地平線が1度左回転する。
これは、星の出が日に1度早くなることに相当し、地球の年周運動を表している。この時の可視範囲は、m=139~322となる。
この結果、二十八宿の見える範囲は下式で表される。
m=(( n+ 91)~(n +274)) (mod365) (9)
これにより、午前0時に見ることのできる二十八宿が次々に算出できる。
その結果を、前掲の表4に四角の囲み文字の間隔で示す。
天文ソフトの計算結果とかなり一致しているというべきであろう。
<二十八宿円盤で得られた天文データの六壬式盤への反映>
①宿盤により一年365日の午前0時に出現する二十八宿をすべて求める。
②上記の結果と六壬式盤で機械的に求められる結果を照合し、近似的に共通する通日を求める。
③上記通日を暦(月日)に変換し、天文学的な理論値とする。
④上記の理論値を、二十四節気と関連付けされた節月の暦にアレンジする。
7 二十八宿円盤における合同式の一般化と精度
最初に二十八宿円盤(宿盤)の合同式を一般化するために、太陽時と恒星時の関係を求める。
<宿盤における1度の時間間隔>
宿盤の恒星時は24時間×60分/365 =3.94521分である。
宿盤の恒星時を地球の太陽時に変換すると
地球の太陽時 (24時間×60分/365) ×365.2422 / (365.2422+1) =3.93443分
これを、宿盤の太陽時の単位時間としてtp=3.9344分と定める。
本稿ではtp =3.9344分を演算の単位時間として、宿盤上の演算はtpにデジタル化して行う。
これは、 数学的には巡回群における正365角形の生成元として扱われる。
即ち、宿盤上の演算におけるp時とは、p×tp=p×3.9344分を意味する。
<宿盤における1太陽日>
24時間×(365+1)/ 365=24h03m56.71233s恒星時
<地球における1平均太陽日>
24時間×(365.2422+1)/ 365.2422=24h03m56.55536s平均恒星時
<恒星時差vd>
宿盤の1太陽日は地球の1平均太陽日より0.15697s進むことがわかる。
これを、宿盤と地球の恒星時差vd=0.15697s と定める。
ここで、通日度数nを時刻度数pに読み替えて、通日n日午前0時に時刻度数pを付加したものを合成時間度数としてnp(n , p)で表記すると、
通日n日のp時における星空は、次の合同式で示される。
np(n , p) ≡ (n+ p )(mod365) (10)
これは、宿盤において通日nを基準点に置いた後、さらに時刻pを加えて地平盤を左回転させることを意味している。
もちろん、この合同式は加法だけでなく減法も演算可能である。
すべての星は一日で全天を移動する。日々において変わるのは出現時刻のみである。
上式は任意の通日と通日における星空の合同性を演算するもので、宿盤の数理的基礎をなすものである。
ところで、図5の星座早見盤を見ると月日と時刻の二つ目盛がある。
これらは、地球の自転量に還元することにより次のように一元化される。
今、任意の起算日における通日第1日の午前0時から通日n日のp時までの経過時間をTtとすれば、
Tt はtpを宿盤の単位時間として下式で表される。
Tt=366×(n-1)+p (11)
その時のnp(n , p) は、初期値の通日1にTtを加算して
np(n , p)≡(1+Tt)(mod365)≡(1+366×(n-1)+p)(mod365)
≡(1+(365+1)×(n-1)+p )(mod365)
≡(1+365×(n-1)+(n-1)+p)(mod365) ≡(n+p)(mod365)
つまり、上述の(10)式np(n , p)≡(n+p)(mod365) が導き出される。
これは、地球が1日に1回転と1度ずつ自転しながら公転軌道を1日に1度回る様を表現している。
(n+p)が同じであれば、星空も同じである。
通日n日p時の星空は、通日(n+k)日における(p-k)時の星空と等しい。
ここで(10)式について、その演算方法と精度について検討しよう。
合同式は、平均太陽の天の赤道における完全な等速運動が前提となるから、
地球の自転角に対応した時刻系であるUT1はそれにふさわしい。(注)
(注)UT1における平均太陽の赤経αsは、2000年1月1日12時UT1を元期とする
ユリウス世紀Tにて以下のように表される。(文献14)
αs=18h41m50.54841s+8640184.812866s×T+0.093104s×(T2乗)-0.0000062 s×(T3乗) (12)
ここで、平均太陽が天の赤道を厳密な意味で等速運動するためには、
歳差の永年加速成分[0.093104s×(T2乗)-0.0000062s×(T3乗)]の影響が無視できる状況にあることが前提となる。
まずは平均太陽時から説明する。
原理的な解説であるので、星空の年代は精度の高い直近の2000年1月1日を通日n=1に設定する。
1月1日の午前0時には、子午線の近くにシリウスが輝いている。
この星空と同じ星空の月日と時刻を(10)式を使っていくつか求めて見よう。
表6は(10)式による演算を行った後、天文ソフトで確認したシリウスの時角と視赤経の変化である。
表6 合同式で求めた同じ星空におけるシリウスの時角と視赤経の変化
時角の累積差は通日n=1を基準 観測地 明石市(東経135° 北緯34°39′)
np(1 , 0) ≡np(74 , 292) ≡・・・≡np(366 , 0) ≡(365+1) (mod365) ≡1
|
通日 n |
合同式 np(n , p) |
2000年 閏年 |
時刻JST p×tp(3.9344分) |
時角の変化 |
視赤経の変化 (注) |
|
|
時角 |
累積差 |
|||||
|
1 |
(1 , 0) |
1月1日 |
00時00分00秒 |
23h53m13s |
- |
06h45m09.6s |
|
74 |
(74,292) |
3月14日 |
19時08分51秒 |
23h53m02s |
-11s |
06h45m09.1s |
|
147 |
(147,219) |
5月26日 |
14時21分38秒 |
23h52m51s |
-22s |
06h45m08.0s |
|
220 |
(220,146) |
8月7日 |
09時34分25秒 |
23h52m39s |
-34s |
06h45m08.6s |
|
293 |
(293,73) |
10月19日 |
04時47分13秒 |
23h52m26s |
-47s |
06h45m10.5s |
|
366 |
(366,0) |
12月31日 |
00時00分00秒 |
23h52m13s |
-60s |
06h45m12.2s |
(注)視赤経は歳差により単調に増加するように思えるが、天文ソフトで1年間の短い期間を見ると、
年周光行差の重畳等の影響により視赤経が減少する時がある。
表6の時角の累積差を見ると、通日の増大に従って単調に減少していることがわかる。
この大部分は、前述の恒星時差vd=0.15697sによるものである。
即ち恒星時差による365日間の累積時角差は、0.15697s×(366-1)日=57.3sとなる。
累積時角差60 sの残り2.7 sは歳差章動によるもので、表6からシリウスの視赤経の一年間の増加分は2.6sとなる。
赤経の増加分は時角の減少、赤経の減少分は時角の増大に作用する。
二十八宿の場合、目安として1年あたりの時角の変化は60s程度、視赤経の変化は2~4 s 程度である。
60sを少し超える程度であれば、角度にして0.3°以下であるから見た目では星の位置は変わらないと言ってよいだろう。
先ほどの説明はnが小さいためやや分かりにくいと思われるので、nを約100年間のレンジに拡大した具体例を示す。
1900年1月1日をn=1として、np(1 , 0) ≡1を想定する。
通日n=1+365×100=36501日は1999年12月8日で、合同式で表せばnp(1 , 0) となる。
天文ソフトにてシリウスの上記時刻の時角と視赤経の変化量を求める。
1900年1月1日 0時0分0秒 時角 23h58m30s 視赤経06h40m46.8 s
1999年12月8日0時0分0秒 時角 22h18m36s 視赤経06h45m09.3s
変化量 時角Hd=5994s 視赤経αd =262.5 s
100年間の恒星時差による時角差vd(n-1)は0.15697s×(36501-1) 日=5729.4sで、
視赤経の変化量αd =262.5 sと合わせて5992sとなる。
この値は、天文ソフトより求めた時角の変化量Hd=5994sとよく一致していることがわかる。
このため以後、恒星時差と視赤経の変化量の和を時角補正値と呼ぶ。
これまでは、平均太陽時を使った場合の検討であった。
古代において平均太陽時は存在しないので、ここで視太陽時を使った場合の検討を行う。
考え方として、視太陽時はまず平均太陽時に変換してから上述の合同計算を行い、
その結果を再び視太陽時に変換すればよい。(ケースA)
この時、宿盤の操作にならって視太陽時で合同計算し、その結果を視太陽時としたもの(ケースB)と比較すると、
視太陽時を使用した宿盤の最大誤差は均時差の正負の最大幅に約1分の時角補正値を付加したものとなる。
やや抽象的な説明と思われるので具体例を挙げる。
均時差の大きな2000年2月4日(立春)と11月7日(立冬)における上述のAとBの2ケースについて合同計算を行う。
通日は表6と同じく1月1日をn=1とする。
<ケースA> ①視太陽時→②平均太陽時→③合同計算→④平均太陽時→⑤視太陽時
① 2000年2月4日(立春)n=35 視太陽時0時00分00秒
② 平均太陽時0時13分49秒 均時差-13分49秒(-3.512 tp)
③ 2000年11月7日(立冬)n=312 np(35 , 0+3.512) ≡np(312 , 88+3.512)
④ 88 tp+3.512 tp =91.512 tp =平均太陽時6時00分2.7秒
(注)天文ソフトによれば、2月4日と11月7日の平均太陽時の合同計算におけシリウスの時角差は45s
⑤ 視太陽時は6時16分21.7秒 均時差+16分19秒
<ケースB> ①視太陽時→②合同計算→③視太陽時(均時差を考慮しないケース)
① 2000年2月4日(立春)n=35 視太陽時0時00分00秒
② 2000年11月7日(立冬)n=312 np(35 , 0) ≡np(312 , 88)
③ 88 tp=視太陽時5時46分13.6秒
ケースAとBの視太陽時の差は6時16分21.7秒-5時46分13.6秒=30分8.1秒となる。
これまでの計算過程から明らかなように、30分8秒は均時差13分49秒と16分19秒の合計であることがわかる。
図13は天文ソフトの太陽の南中時間から得られたBC172年頃の均時差(太線)である。
細線は、比較のためのAD2000年の均時差である。
均時差曲線は、長年月の間には地球の公転運動における中心差等により変化する。
BC172年頃の黄道傾斜角は23.7°(現在23.4°)、近日点は黄経246°(現在284°)付近にあり、
軌道の離心率eは0.0176(現在0.0167)程度と推定される。
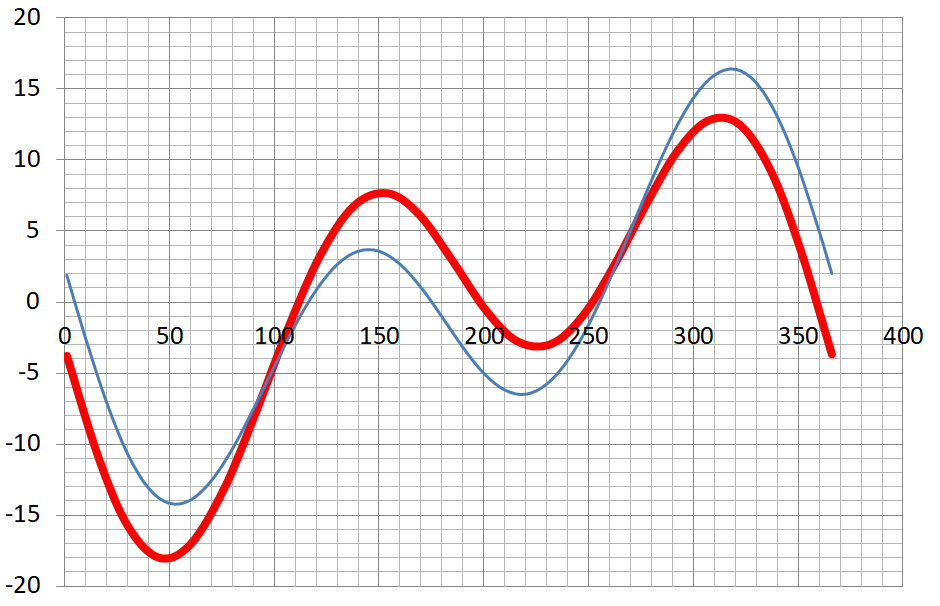
図13 均時差(太線):BC173年冬至~ 均時差(細線):AD2000年冬至~
平均太陽時間=視太陽時間-均時差
横軸(太線):BC173年12月24日冬至を第1日とする通日(1日~366日)
横軸(細線):AD2000年12月21日冬至を第1日とする通日(1日~366日)
縦軸:均時差(分)
図13から、BC172年頃の宿盤の最大誤差は、
均時差の正負の最大幅に約1分の時角補正値を付加した13分+18分+1分=32分程度となる。
8 まとめ
(1)六壬式盤の天盤の暦は太乙九宮占盤の冬至起算の平気法による節切りを踏襲したもので、
二十八宿の表示は二十八宿円盤の天文データをもとに作成された。
(2)六壬式盤の月日を地盤の子の位置に合わすと、
天盤の上半部にその月日の古代中国における一日の始まりである夜半(午前0時)に展開している二十八宿が表示される。
(3)二十八宿円盤(宿盤)は古代中国の二十八宿早見盤である。
現在の星座早見盤に対応させれば、星座盤が下盤、地平線が描かれた地平盤が上盤に相当する。
操作は星座盤でなく、地平盤を回転させる。
(4)宿盤の二十八宿の運行は、基本的に宿盤の恒星時を地球の太陽時に読み替えたものを単位時間としてデジタル化することにより、
365を法とする次の合同式で表される。
下式は任意の通日と通日における二十八宿の星空の合同性を演算するもので、宿盤の数理的基礎をなすものである。
np(n , p) ≡ (n+ p )(mod365)
n:任意の起算日からの通日 p:3.9344分を単位時間とする時刻
上式は平均太陽時ではnとpの和が等しければその星空は見た目には同一となるが、視太陽時では均時差の補正を必要とする。
9 参考文献
1山田慶兒:制作する行為としての技術、朝日新聞社、①187-188 ②199 ③205-212 ④197 ⑤190-196 ⑥201、(1991)
2安徽省文物工作隊・阜陽地区博物館・阜陽県文化局:阜陽(ふよう)双古堆西漢汝陰侯墓発掘簡報、(『文物』、1978年8期、12-25)
3殷涤非(いんじょうひ):西漢汝陰侯墓出土的占盤和天文円儀、(『考古』、1978年5期、338-343)
4潘鼐(はんだい):我國早期的二十八宿觀測及其時代考、(『中華文史論叢』1979年第3輯、163-164)
5松岡秀達:安倍晴明「占事略决」詳解(計算ソフト付)、岩田書院、(2007)
6小坂真二:安倍晴明撰『占事略決』と陰陽道、汲古書院、 ①15 374 ②13-15、(2004)
7甘粛省博物館:武威磨咀子三座漢墓発掘簡報、(『文物』、1972年12期、9-15)
8薮内清:新天文学講座1 星座、恒星社厚生閣、 133-137、(1964)
9諸橋徹次:大漢和辞典、巻十 664 ・654、巻七 542、大修館書店、(1985)
張揖(ちょうゆう)・王念孫:廣雅疎證 巻九上 「營室謂之豕韋」、台湾商務印書館、1093 (1968)
10鎌田正:春秋左氏伝三 新釈漢文大系32、明治書院、1362-1363、(1994)
11岡田芳郎編:暦の大事典、朝倉書店、232、(2014)
12暦の会編:暦の百科事典、本の友社、63、(1999)
13薮内清:増補改訂 中国の天文暦法、平凡社、307、(1990)
14磯部琇三(しゅうぞう) [ほか]、天文の事典、朝倉書店、634、(2003)
10 参考サイト
HP1日本天文学会『天文学辞典』「天体暦」 http://astro-dic.jp/ephemeris/
HP2橋本敬造「先秦時代の星座と天文觀測」京都大学学術情報リポジトリ
https://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/66604/1/jic053_189.pdf
『東方學報』京都 第53冊、189-232、京都大学人文科学研究所、(1981)
HP3「新儀象法要+簡平儀說」中國哲學書電子化計劃 http://ctext.org/library.pl?if=gb&file=86840&page=68
HP4「每日頭條」 https://kknews.cc/news/avpla6j.html
HP5「呂氏春秋 孟春紀 正月紀」中國哲學書電子化計劃 https://ctext.org/lv-shi-chun-qiu/meng-chun-ji/zh
関連論文 キトラ古墳天文図における装飾絵画表現と太初暦紀年法
渾天説の曙 曾候乙墓出土漆箱二十八宿図の天文学的メカニズム
トップページに戻る (C20190610
)